
MD-Appendix 2: Post Formal Thought and Thinking Outside the Box



Join the nine dots in a 3-by-3 two-axis grid using four straight lines without:
The nine dots are on a plane surface.
Hint: The puzzle is hard and demands out-of-the-box thinking.
Soon you figure out that the puzzle is hard. To solve it, you may choose either trial and error or systematic reasoning.
As trial and error is arbitrary with no certainty of result within a reasonable time, it is eventually rejected.
The first step in any serious problem-solving task is to perform a quick trial, analyze the results of the trial, and draw a key conclusion.
As a first trial, the nine dot are joined in the simplest possible manner.
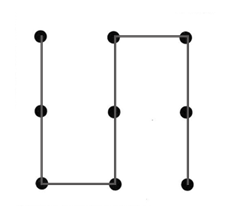
What clues can we get from this simple trial?
Observation: To connect the nine dots, three independent straight lines each joining three dots are used. But to connect the three lines, two more straight lines are used. The solution is invalid because it has five straight lines.
Reasonable conclusions that may be made:
Conclusion 1: There are two groups of lines to analyze—the primary lines joining the dots, and the secondary lines joining the primary lines. In this trial, we used three primary lines and two secondary lines.
Conclusion 2: Secondary lines do not contribute to joining more dots, so they are wasteful. The number of secondary lines should be minimized. Ideally, there should be zero secondary lines.
Observation: A property of the connections not considered so far is the angle of the lines. All five lines in the figure are directed vertically or horizontally with no oblique angles.
Conclusion 3: Whichever way you join the dots with these mutually perpendicular sets of lines aligned with the two axes, a solution cannot be reached. At least one line must be oblique. Such an oblique line reduces the number of wasteful secondary lines by one.
To try out these new ideas, we need a second experiment.
It is identified that the most efficient oblique line joins three dots.
Conclusion 4: One primary line in the solution must be one of the two diagonals.
Where should the pencil move after joining three diagonally placed dots?
Conclusion 5: It can only be along one of the two adjoining mutually perpendicular outer boundary sides of the grid. This directly contributes to a better solution by reducing the number of secondary lines (joining two primary lines) by one.
The result of this action is shown below:

Conclusion 6: The two lines, one diagonal and the other a vertical, join five dots. This combination must be a part of the final solution.
Now, how do we connect the remaining four dots and join the resulting lines with the two existing lines?
Let us complete this second trial by joining the remaining four dots in a simple fashion. The result is shown below.

When a problem demands an out-of-the-box idea to solve it, usually, a property of the primary entity in the obstacle (in our problem, a joining line) is invisible. As a result, the choice of considering this invisible property is overlooked. If the obstacle can only be overcome by adjusting (or changing) this overlooked property, the problem will prove impossible to solve (as long as this property is ignored).
Let us list the properties of our main entity, the joining line:
Are there any other properties of the joining lines? Have we taken any properties for granted and forgotten we can change them?
Do we always have to draw a line inside the 3-by-3 grid-box? Is this a must? Insistent questioning brings out new ideas. The property that was invisible has been identified.
What is meant by this is shown below.

Lines in the solution are assumed to be restricted to the grid-box.
Can’t a joining line pass over a dot at the border and continue outside the grid-box to connect with a second extended line? Well, surely it can. Nobody prohibits this.
More importantly,
If two primary lines continue beyond the grid-box and join each other, it saves a precious extra line used for linking the two.
This must be the sought after change in a property. And it should be part of the key pattern as well.
Key pattern: At least two lines must continue beyond the last dot they join and move out of the grid. Two lines, because, as a line continues beyond the grid, it must return to the grid by joining with a second line also beyond the grid.
The key pattern shows the way forward, but not the direct solution.
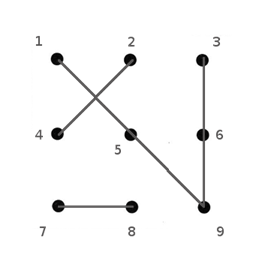
For convenience of understanding, the two lines joining five dots in the grid are shown with the dots labeled below.

The pencil starts from dot 1, moves over five dots, and stops at dot 3. Five dots are connected without violating a condition and four dots stay unconnected.
The analysis and joining actions are now segment by segment: we will join the four remaining dots with independent line segments first, then connect the segments.
How many line segments are needed to join these four dots?
Conclusion 7: The only way to join the two remaining pairs of dots so far is by two independent line segments. We cannot use one or three lines.
This conclusion is shown below:
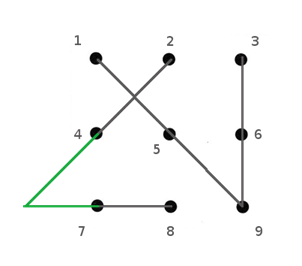
The final challenge is to connect the four lines.
Observation: Nine dots are already joined by four line segments. The quota of line segments is exhausted. The segments must be joined without adding line segments. How do we connect line segment 2-4 with line segment 8-7?
Conclusion 8: Extend line segment 2-4 and line segment 8-7 until the two meet at a point outside the grid-box.
The two disconnected line segments are now joined.
Now, the problem is reduced to connecting dot 2 with dot 3 using no additional line segments. This is easy with the same technique.
Conclusion 9: Extend line segment 4-2 and line segment 6-3 to meet at a point outside the grid-box.
The solution has finally been reached.
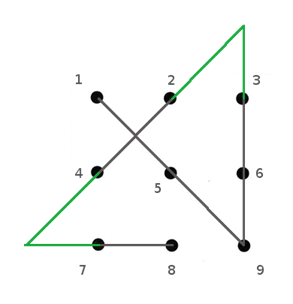
All four connecting lines move out of the grid-box to join with each other. This is truly an out-of-the-box solution.
Where should the pencil start? We have two choices.
We may start at dot 1 and end at dot 8, or start at dot 8 and end at dot 1. Both methods produce the same result.
An alternative method is to start by connecting the diagonal sequence 3-5-7.
This appears to be a second solution. Furthermore, if you rotate one of the two, it coincides perfectly with the other.
This means only one rotationally unique solution is possible.
The critical breakthrough in this hard puzzle is found with the help of property analysis to find the taken-for-granted, invisible property of an obstacle or element. This is a powerful inventive technique.
Try this inventive technique when you are faced with an impenetrable barrier while solving a hard problem, in academia or in real life.
This classic riddle is one-of-a-kind with no easy or intuitive solution. Finding a solution through random trial is hard, if not impossible. The solution requires elusive, out-of-the-box thinking sought after all over the world. To find it, the inventive Property Change Analysis Technique is used to uncover an out-of-the-box, unthought-of possibility.
Question: Draw nine dots on a piece of paper. Can you connect the nine dots with three straight lines without lifting your pencil from the paper?
Question: Draw nine dots on a piece of paper. Can you connect the nine dots with two straight lines without lifting your pencil from the paper?
Question: Draw nine dots on a piece of paper. Can you connect the nine dots with one straight line without lifting the pencil from the paper?
Some people argue that circles have no sides. Others argue that circles have one side. Is it possible that circles have an infinite number of sides?
Start by asking the question, "How many sides does a triangle have?" Then, ask the question, "How many sides does a square have?"
Einstein said, "All straight lines at infinity are great circles."
Einstein then said, "Therefore, if you looked infinitely far ahead in a straight line, you would eventually see the back of your head!"
Question: The instant-by-instant timeline of our 4th dimensional existence is also a line. Therefore, if we look far enough into the future, what do you think we will see?
Question: Therefore, to go time travelling into the past, we must time travel into the ____________? We do this by travelling faster than the speed of ____________.